До сих пор в системе мы рассматривали силы, приложенные к твердому телу в какой-либо его точке. Такие силы называются сосредоточенными.
Однако в инженерных расчетах часто приходится встречаться с нагрузками, распределенными вдоль данной поверхности или линии по тому или иному закону. Распределенные силы прежде всего характеризуются интенсивностью q, т.е. величиной силы, приходящейся на единицу поверхности или линии.
Так как все аксиомы и теоремы статики получены для сосредоточенных сил, то необходимо рассмотреть способы перехода от распределенных сил к сосредоточенным в простейших, часто возникающих случаях.
1) Силы, равномерно распределенные вдоль отрезка прямой (рис.5.4).
 |
Рис.5.4.
Понятно, что q — здесь величина постоянная. При статических расчетах эту систему сил можно заменить сосредоточенной силой (ее равнодействующей), которая по модулю равна
Q = q × a и приложена в ее середине.
2) Силы, равномерно распределенные вдоль отрезка прямой по линейному закону (рис.5.5). Например, силы давления воды на плотину, которые имеют наибольшее давление у дна и равны нулю у поверхности воды. Здесь q-величина переменная, принимающая значения 0£q£qmax.
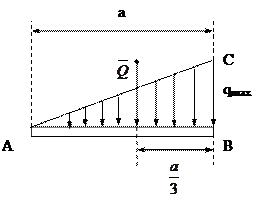 |
Рис.5.5.
Равнодействующая такой распределенной нагрузки по модулю равна
Q= 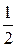 aqmax,
aqmax,
а ее линия действия проходит через центр тяжести треугольника АВС, который находится в точке пересечения медиан, т.е. линия действия силы Q проходит на расстоянии 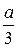 от стороны ВС треугольника АВС.
от стороны ВС треугольника АВС.
3) Силы, равномерно распределенные по дуге окружности (рис.5.6)
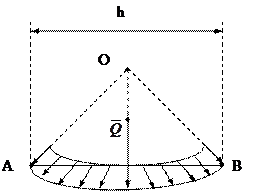 |
Рис.5.6.
Примером таких сил могут служить силы гидростатического давления на боковые стенки цилиндра.
Равнодействующая таких сил по модулю равна
Q = q × h,
где h-длина хорды, стягивающей дугу АВ. Направлена сила 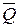 по оси симметрии дуги окружности.
по оси симметрии дуги окружности.
В заключение в качестве примера рассмотрим еще один вид связи — жесткую заделку конца балки (рис.5.7).
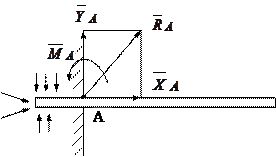 |
Рис.5.7.
Такая опора не допускает не только линейных перемещений балки, но и ее поворота. На заделанную часть действуют со стороны стены неравномерно распределенные силы. Пользуясь леммой о параллельном переносе силы, их можно привести к точке А и заменить одной силой 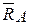 и одной парой с моментом MA. Нахождение неизвестной по модулю и направлению реакции
и одной парой с моментом MA. Нахождение неизвестной по модулю и направлению реакции 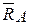 в свою очередь можно заменить нахождением двух ее составляющих
в свою очередь можно заменить нахождением двух ее составляющих 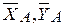
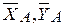 , MA.
, MA. Действие нескольких сосредоточенных сил
Задача о действии одной сосредоточенной силы
Напряжения в грунтовом массиве от действия сосредоточенной силы
Фазы напряженНого состояния грунта.
Определение напряжений в массиве грунта.
Лекция № 3
Задача о действии одной сосредоточенной силы (задача Буссинеска), нескольких сил и любой распределенной нагрузки на плоское полупространство. Задача о действии местной равномерно распределенной на прямоугольной площади нагрузке (строгое решение А. Лява) и метод угловых точек. Эпюры сжимающих напряжений и влияние площади загрузки.
Концентрированная нагрузка — это сила, приложенная в одной точке на балке или конструкции. Балки обычно используются для структурной поддержки в домах, коммерческих зданиях и мостах. Луч должен быть спроектирован так, чтобы выдерживать силы и напряжения, при этом минимизируя вес, требования к пространству и стоимость материала. Неправильно спроектированные лучи могут выходить из строя досрочно и иметь катастрофические последствия.
Нагрузка или сила могут быть сконцентрированы или распределены. Распределенная нагрузка распределяется по большой площади. Он может быть равномерно распределен, причем величина силы одинакова во всей области, к которой она применяется; или неравномерно, что означает, что оно не равномерно распределено. Распределенная нагрузка будет влиять на конструкцию луча иначе, чем на концентрированную нагрузку. Концентрированный может быть применен в более чем одном месте на балке, и на одном пучке могут существовать многочисленные точки нагружения.
(задача Ж. Буссинеска)
Рассматривается действие сосредоточенной силы Р, приложенной перпендикулярно к ограничивающей полупространство плоскости. Полупространство однородно в глубину, в стороны и обладает линейной деформируемостью (рис. 3.1).
В действительности все нагрузки применяются в некоторой конечной области по сравнению с одной точкой. Когда площадь мала, обычно считается сосредоточенной нагрузкой, что упрощает расчеты инженерного проектирования. Например, вес человека на конце дайв-доски будет считаться сосредоточенным видом нагрузки, хотя вес человека действительно распределяется только по площади, покрытой нижней частью его ног.
Двумя наиболее важными характеристиками сосредоточенной нагрузки являются величина силы и место ее применения. Как поддерживается луч или структура, играет важную роль в его способности поддерживать этот тип нагрузки. Концентрированная нагрузка, приложенная в центре длинного луча, поддерживаемая на обоих концах, будет вести себя по-разному, чем та же самая нагрузка, приложенная к концу консольного пучка.
Рис. 3.1. Расчетная схема действия сосредоточенной силы
Для любой точки полупространства с координатами Z, Y или b, R (к примеру М 1 и М 2) перемещения точек по направлению радиуса R равны:
; . (3.1)
Концентрированная нагрузка может привести к тому, что луч будет отклоняться или изгибаться при приложении силы. Конструкция и конструкция балки будут влиять на его способность противостоять изгибу при воздействии такого веса. Прогиб пучка является функцией его поперечного сечения, его поддержки, материала, из которого он изготовлен, и где применяются силы. чаще всего используются в коммерческих зданиях из-за их прочности и устойчивости к изгибу, но балки также изготавливаются с использованием других материалов, таких как дерево и алюминий.
Относительная деформация грунта на отрезке dR :
Для линейно деформируемой среды напряжение пропорционально деформации
, (3.3)
где — коэффициенты пропорциональности.
Напряжения в массиве грунта связаны с величиной силы Р условиями равновесия. Важно заметить, что для составления уравнения равновесия проведем полушаровое сечение с центром в точке приложения сосредоточенной силы (рис. 3
Замена распределенных сил сосредоточенной равнодействующей возможна только в том случае, когда производится анализ работы бруса в целом, т. е. в объемах, существенно превышающих объем [c.14]
В рассматриваемых ниже задачах используются лишь зри разновидности нагрузок сосредоточенные силы, равномерно распределенные силы и пары сил (сосредоточенные моменты) .
Выше указывалось, что резьба с треугольным профилем является основной крепежной резьбой. Целесообразность этого очевидна из сравнения треугольной и прямоугольной резьбы. Осевая сила Т (рис. 3.20) вызывает между витками резьбы винта и гайки нормальные к боковой поверхности профиля резьбы силы взаимодействия Ri и Считая условно эти силы сосредоточенными, получим выражение для суммарной окружной силы трения в резьбе (без учета угла подъема) [c.279]
Пусть на участке АВ прямой линии длиной I распределены параллельные силы, интенсивность которых д постоянна (рис. 48, а). Заменим эти распределенные силы сосредоточенными. Для этого отрезок АВ разобьем на отрезки достаточно малых размеров по сравнению с его
Формула (3.59) решает поставленную задачу о приведении приложенных к элементу распределенных сил к системе сил, сосредоточенных в вершинах. [c.139]
Это — уравнение равновесия под действием сил, сосредоточенных вдоль оси г с объемной плотностью [c.157]
Решение.. Заменим распределенные силы сосредоточенными силами. Рассмотрим прежде всего силы, распределенные вдоль прямого отрезка АЕ по линейному закону. Для этих сил интенсивность q является величиной переменной, растущей от нуля до максимального значения Равнодействующая будет определяться анало- [c.111]
Для этого заменим распределенные силы сосредоточенными, а также отбросим все внешние связи и заменим их действие на сочлененную систему реакциями связей (рис. 83, б). [c.115]
Определение частот колебаний прямолинейного естественно закрученного стержня постоянного сечения (см. рис. 7.2), нагруженного при е= 1 сосредоточенной осевой силой сосредоточенным крутящим моментом При [c.185]
F — внешняя сила сосредоточенная нагрузка [c.4]
Полученные сведения позволяют перейти к построению эпюр. Рекомендуем сначала рассмотреть три простейших случая нагружения балки, жестко защемленной одним концом парой сил, сосредоточенной силой и равномерно распределенной по всей длине балки нагрузкой. При построении этих простейших эпюр надо не просто пользоваться правилами для нахождения величин (Э и Л4, а изображать отдельно оставленную часть балки и находить Q и из уравнений равновесия. [c.123]
Равнодействующая нормальных сил упругости в сечении называется продольным усилием. Продольное усилие определяется методом сечений. Величина продольного усилия в каком-нибудь поперечном сечении стержня равна алгебраической сумме всех внешних продольных сил (сосредоточенных Р и распределенных по произвольному закону с интенсивностью q ), действующих на стержень по одну сторону от рассматриваемого сечения. Растягивающее усилие считается положительным, сжимающее — отрицательным. [c.10]
Крутящий момент определяется методом сечений. Величина крутящего момента в каком-нибудь поперечном сечении стержня равна алгебраической сумме моментов всех внешних пар сил (сосредоточенных М. и распределенных по длине с интенсивностью tti), действующих относительно геометрической оси стержня по одну сторону от рассматриваемого сечения [c.74]
Величина поперечной силы Qj. в каком-нибудь сечении балки равна алгебраической сумме проекций всех внешних сил (сосредоточенных и распределенных), действующих на балку по одну сторону от рассматриваемого сечения на одну из главных центральных осей инерции сечения. [c.93]
Эпюры Mr и AJg приведены на рис. 480, б (штриховые линии у оси пластинки соответствуют силе, сосредоточенной в точке). [c.521]
Сила сосредоточенная в бесконечном теле 393 [c.574]
Как правило, мы имеем дело всего с тремя типами обобщенных сил сосредоточенный внешний момент, сосредоточенная сила и равномерно распределенная на некотором участке нагрузка интенсивности q. Каждой из обобщенных сил свойствен определенный вид эпюры изгибающих моментов. [c.53]
Компоненты вектора сил сосредоточенные силы, тепловые нагрузки, давления и силы инерции. В процессе анализа можно учитывать такие нелинейные свойства, как пластичность и ползучесть материала, большие прогибы, большие деформации и контактное взаимодействие при условии, что нагрузки возрастают постепенно. [c.60]
Метод сечений. Пусть на элемент конструкции, условно изображенный на рис. 2.1, а, действуют внешние силы (сосредоточенные или распределенные на участках поверхности). Считаем, что элемент конструкции под действием указанных сил находится в равновесии. Проведем плоскость П, которая рассечет элемент на две части, и рассмотрим одну из частей, например левую (рис. 2.1, б). [c.23]
Подставим значения постоянных С и D в уравнение углов наклона касательных и в уравнение прогибов участка V, как в наиболее общие уравнения, содержащие все изгибающие факторы (пару сил, сосредоточенную нагрузку и распределенную нагрузку). [c.255]
Наиболее универсальным приемом здесь является введение сосредоточенных сил, заменяющих некоторые распределенные нагрузки. Такого рода упрощение применимо, понятно, только в том случае, если размеры поверхности, по которой происходит передача усилий, малы по сравнению с общими размерами конструктивного элемента. Ясно, что в реальных конструкциях передача усилий в точке неосуществима, и сосредоточенная сила представляет собой понятие, свойственное только расчетной схеме. Замена распределенных сил сосредоточенной равнодействующей возможна лишь в тех задачах, где анализируется напряженное состояние системы в целом, т. е. в объемах, существенно превышающих объем контактной зоны. [c.17]
Коэффициенты влияния jJ, для углов наклона, вызываемых силами, будут в соответствии с теоремой о взаимности перемещений такими же, как и улч- Центробежные силы сосредоточенных масс при вращении изогнутого вала определяются выражением [c.51]
Распределение напряжений около точки приложения нагрузки примерно такое же, как в круглой пластинке радиуса 0,64 Ь, нагруженной силой, сосредоточенной в центре (см. стр. 165). [c.160]
При этих допущениях коленчатый вал в отношении передачи усилий рассматривается как прямая балка, свободно лежащая на опорах п нагруженная сосредоточенными силами расчет вала производится обычно в предположении, что он разрезан по опорам и нагружен силами, сосредоточенными в серединах подшипников. Влияние на рассчитываемое колено других колен учитывается лишь величиной набегающего момента от соседних цилиндров, расположенных со стороны свободного конца вала. [c.166]
Система загружена горизонтальной силой, сосредоточенной в узле (фиг. 17, в). В этом случае узлы системы смещаются. В ригелях, которые сместятся поступательно, возникнут лишь нормальные усилия. Во всех стойках, верхние концы которых получат одинаковые ио отношению к их нижним защемленным концам смещения Д, возникнут изгибающие моменты и поперечные силы. Если обозначить через и mjj концевые изгибающие моменты, возникающие у нижнего и верхнего концов стоек, а через поперечные силы, возникающие в стойках системы при относительном смещении их концов, равном единице, то формула, определяющая действительную величину смещения системы, примет вид [c.40]
Формула для определения моментов защемления, возникающих по концам стоек от горизонтальной силы, сосредоточенной в верхнем узле системы [c.53]
Р — горизонтальная сила, сосредоточенная в верхнем узле системы [c.54]
Стержневая система загружается силами, сосредоточенными лишь в её узлах. [c.226]
Пара сил (сосредоточенный момент), например, может быть образована двумя одинаковыми грузами F, действующими на тело так, как показано на рис. 95, а. Условное изображение пары сил, действуюптей на тело, показано на рис. 95, б. [c.99]
Пусть на участке АВ прямой линии длиной I распределены параллельные силы, интенсивность которых р постоянна (рис. 54, а). Заменим эти распределенные силы сосредоточенными. Для этого отрезок АВ разобъем на отрезки достаточно малых размеров по сравнению с его длиной. На каждый такой малый отрезок действует сила которую при достаточной малости длины отрезка Д/ можно [c.53]
Если же составить ряд для изгибающих моментов (6.51), то он будет сходиться значительно медленнее, чем для прогибов, в особенности вблизи приложения силы Р, а непосредственно под силой он вообш е расходится — здесь моменты стремятся к бесконечности. Дело здесь не только и не столько в недостатках данного метода решения. Причина данной особенности состоит в самой модели силы, сосредоточенной в точке (рис. 6.29). Если из пластины вырезать вокруг точки приложения силы элемент х х Ai/ и устремить Аа О и Ау то для уравновешивания конечной силы Р интенсивность поперечных сил и моментов Qy, М , Му на гранях этого элемента должна будет возрастать до бесконечности. Действительно, пусть, например, из [c.173]
Эти уравнения имеют вид уравнений, описывающих консервативную систему, на которую действуют как распределенные силы, так и силы, сосредоточенные на концах. В выражения для этих сил входят компоненты с частотами со и Зсо, где со — частота, определяемая соотношением (11.1.23). Так как спектр частот рассматриваемой нами системы неэквидистантен, т. е. Зсо1 т соа, то компонента силы с частотой Зеох не создаст в системе движения с заметной амплитудой. Поэтому эту составляющую силы можно не учитывать. Тогда граничное условие (11.2.3,6) примет вид [c.352]
Нелинейная зависимость между перемещениями оси стержня и продольными силами исключает возможность использования при продольно-поперечном изгибе по отношению к продольным силам принципа независимости действия сил. Вследствие этого расчеты сжато-изогнутых или растянуто-нзогнутых стержней при продольных силах, сосредоточенных и распределенных по длине стержня, резко отличаются друг от друга. Расчет первых сводится к интегрированию линейных дифференциальных уравнений с постоянными коэффициентами во втором случае при распределенных силах приходится интегрировать линейные дифференциальные уравнения с переменными коэффициентами. [c.439]
По назначению резьбы разделяют на крепежные, крепежно-уплотнительные и ходовые. Крепежная резьба должна обладать высокой прочностью и большим трением, предохраняющим соединяемые детали от самоотвин-чивания крепежно-уплотнительные кроме указанных качеств должны обеспечивать повышенную плотность соединения ходовые резьбы должны быть с малым трением, чтобы повысить КПД и уменьшить износ, а прочность во многих случаях не является здесь основным фактором. К крепежным резьбам относят метрические (рис. 194, а) с треугольным профилем к крепежно-уплотнительным — трубная (рис, 194,6) треугольная с закругленными вершинами и впадинами а к ходовым относятся трапецеидальная (рис. 194, в) и упорная (рис. 194,2). На рис. 195 сопоставляются трапецеидальная и метрическая (треугольная) резьбы. Осевая сила Р действующая по стержню винта, воспринимается гайкой через элементарные нормальные силы, распределенные по поверхности резьбы. Считая условно эти силы сосредоточенными, получаем выражение для суммарной окружной силы трения в резьбе (без учета угла подъема) для метри- [c.226]
Изгиб стержня (поперечный) возникает при действии на него сил (сосредоточенных и (или) распределенных), нерпеидикулярных [c.36]
Звенья механизма часто нагружаются силами, сосредоточенными или распределенными, приложенными между шарнирными или узловыми точками (например, распределенными силами будут силы тяжести, силы инерции, а их рав- СЫсатие [c.115]
Проверкана изгиб в сечении АВ. Мостик рассматривается как балка, свободно лежащая на двух опорах и нагруженная силой, сосредоточенной по окружности диа- ф 43 [c.793]
Примечание. Моменты уменьшены в 1000 раз, так как силы, сосредоточенные над опорами, под дейстЕИсм которых они гозниклн, были увеличены в 1000 раз. [c.207]
Сопротивление материалов (1970) — [ c.13 ]
Основной курс теоретической механики. Ч.1 (1972) — [ c.180 ]
Сопротивление материалов 1986 (1986) — [ c.43 ]
Сопротивление материалов (1999) — [ c.17 ]
Сопротивление материалов (1986) — [ c.14 ]
Сопротивление материалов (1976) — [ c.17 ]
Теория упругости (1970) — [ c.497 , c.513 , c.529 , c.531 ]
Сопротивление материалов (1959) — [ c.55 ]
Механика слоистых вязкоупругопластичных элементов конструкций (2005) — [ c.9 , c.23 , c.40 , c.151 , c.212 , c.234 ]
Сопротивление материалов Издание 3 (1969) — [ c.8 ]
Краткий курс теоретической механики 1970 (1970) — [ c.18 ]
Теория упругости и пластичности (2002) — [ c.16 ]
Механика сплошной среды Т.1 (1970) — [ c.133 ]
Сопротивление материалов Том 1 Издание 2 (1965) — [ c.80 , c.128 ]
8 Плоская система сил
Плоская система сил – система сил, расположенных в одной плоскости. Система сил приводится к одной силе – главному вектору и к паре сил, момент которой равен главному моменту. Момент пары сил направлен перпендикулярно к плоскости, в которой лежат силы. В плоских системах нет необходимости использовать векторное представление момента. Теорема Вариньона – если плоская система сил приводится к равнодействующей, то ее момент относительно какой-либо точки равен алгебраической (т.е. с учетом знака) сумме моментов всех сил относит. той же точки.
Метод определения равнодействующей плоской системы сил
Для плоской системы сил проекции главного вектора R на оси координатной системы Oxy и алгебраический главный момент LO относительно центра О определяются по формулам:
Rx = Fix; Ry = Fiy; LO = MO(Fi).
Если для данной системы сил главный вектор R 0, то эта система сил приводится к равнодействующей силе. При этом возможны два случая:
LO = 0. В этом случае система сразу приводится к равнодействующей R, проходящей через центр О.
Пример
LO 0. В этом случае система сил заменяется равнодействующей R* = R, линия действия которой образуется параллельным переносом (см. рис.) линии действия силы R на расстояние d = |LO|/R, где R — модуль главного вектора R. При этом момент силы R* относительно точки О должен совпадать с моментом LO по величине и знаку.
Уравнение линии действия равнодействующей R* имеет следующий вид:
A·x + B·y + C = 0, где A = -Ry; B = Rx; C = LO.
Равнодействующая сила R* может быть приложена к любой точке твердого тела, лежащей на этой прямой.
9Сосредоточенные и распределенные силы, равнодействующая распределенной силы
Сосредоточенными считаются силы, приложенные к малой поверхности, размеры которой малы по сравнению с размерами тела. Однако при расчете напряжений вблизи зоны приложения силы нагрузку следует считать распределенной. К сосредоточенным нагрузкам относят не только сосредоточенные силы, но и пары сил, примером которых можно считать нагрузку, создаваемую гаечным ключом при закручивании гайки. Сосредоточенные усилия измеряются в кН.
Распределенные нагрузки бывают распределенными по длине и по площади . К распределенным нагрузкам относят давление жидкости, газа или другого тела. Распределенные силы измеряются, как правило, в кН/м (распределенные по длине) и кН/м2 (распределенные по площади
Например, на рисунке 1.23, а приведена равномерно распределенная по длине ABнагрузка интенсивностью q , измеряемая в Н/м. Эта нагрузка может быть заменена сосредоточенной силой
Q = q⋅AB [Н],
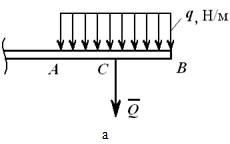
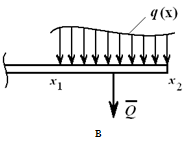
приложенной в середине отрезка AB . На рисунке 1.23, б показана равномерно убывающая (возрастающая) нагрузка, которая может быть заменена равнодействующей силой
Q = qmax⋅AB/2,
приложенной в точке C , причем AC = 2/3 AB .

В произвольном
случае, зная функцию q(x)
(рисунок 1.23, в), рассчитываем эквивалентную
силу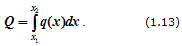
Сосредоточенные силы
Cтраница 1
Сосредоточенные силы, которые мы получали при замене моментов Н соответствующим распределением перерезывающих сил, являются следствием изломов в контуре пластинки. Если контур пластинки представляет собой плавную кривую, мы получим лишь непрерывное распределение перерезывающих сил интенсивности ( ШУ, где s — элемент дуги контура. [1]
Сосредоточенные силы представим как частный случай массовых сил. [2]
Сосредоточенные силы, соответствующие двум смежным краям-суммируются в этом угле, образуя таким образом суммарную поперечную силу, приложенную к углу и равную, как показано на рисунке, удвоенной величине, которую принимает момент Мху в угловой точке. [3]
Сосредоточенные силы Z, сжимающие шар, приложены в его полюсах. [4]
Сосредоточенные силы Q ( рис. 26), передающиеся от болтов кольцам фланцев, вызывают неравномерный по окружности прогиб этих колец. В зависимости от шага болтов, толщины кольца, размера и конструкции фланца этот неравномерный прогиб может привести к столь неравномерной передаче давления на прокладку, что будет затруднительно уплотнить фланце вое соединение. [6]
Сосредоточенные силы Q ( рис. 38), передающиеся от болтов кольцам фланцев, вызывают неравномерный по окружности прогиб этих колец. [8]
Наши сосредоточенные силы могут рассматриваться как предел сплошных нагрузок, распределенных на протяжении очень небольших дуг. [9]
Если сосредоточенные силы и моменты, вызывающие изгиб, кручение и растяжение ( сжатие), расположены в различных плоскостях, то их следует разложить на составляющие, лежащие в двух взаимно перпендикулярных плоскостях, и в каждой из этих плоскостей определять реакции опор и внутренние нагрузки. Если наибольший угол между плоскостями, в которых расположены нагрузки, не превышает 30, то можно принимать все силы и моменты лежащими в одной плоскости. [10]
Эти сосредоточенные силы в ближней узловой точке k — то стержня должны вычитаться из полученных усилий, давая характерные скачки в эпюре. [11]
Эти сосредоточенные силы предполагаются приложенными к мысленно выделяемым из всей пространственной системы поперечным вертикальным многоэтажным жестким рамам, имеющим жесткую заделку и пятах. В целях облегчения собственного веса перекрытия железобетонные плиты иногда выполняются из шлако-железобетона. [12]
Эти сосредоточенные силы отстоят друг от друга на расстоянии, равном длине или ширине пластины, поэтому принцип Сен-Венана мало что дает в смысле обоснования того, что было сделано. Эти силы обычно не столь важны, если углы оперты или защемлены, так как при этом они не могут влиять на прогибы пластины, а величина реакций, как правило, не является критической. Приведенная поперечная сила является хорошей аппроксимацией при вычислении прогибов или критических нагрузок, которые зависят от условий, осредненных по всей пластине. [13]
Две равные сосредоточенные силы, приложенные симметрично относительно центра струны. [14]
Рм — сосредоточенные силы; q, q № — интенсивности распределенных нагрузок; /, 1М — линейные размеры пластин. [15]
Страницы: 1 2 3 4
Заметим, что перемещение под сосредоточенной силой обращается в бесконечность, что влечет за собой также нарушение фактической совместности деформаций . [c.15]
Мы считаем, однако полезней, рассматривая вынужденное колебание, сначала решать задачу для сил, сосредоточенных в одной точке, а затем уже для сил сосредоточенных на малой площади. Результат этого допущения скажется в том, чго форма мембраны будет иметь острый пик бесконечной высоты в точке приложения силы. Затем мы срежем остриё пика до такой высоты, чтобы площадь вершины срезанного пика была равна действительной площади приложения силы (это показано на фиг. 35). [c.200]
Если плёнка материала имеет некоторую жёсткость, то сила, сосредоточенная в точке, не будет давать бесконечного смещения. Но если нет значительной жёсткости, то смещение точки прило-л ения будет значительно больше, чем смещение на остальной площади. [c.200]
Эпюры, построенные по этим формулам, представлены на рис. 353. Как видим, в центре изгибающие моменты обращаются в бесконечность, что является следствием того, что здесь обращается в бесконечность поперечная сила р. В центре, таким образом, имеет место, как говорят, неустранимая особенность. В реальных условиях сосредоточенных в точке сил не существует — это лишь схема. Сила прикладывается по небольшой площадке (рис. 354), в зависимости от величины «которой будут возникать большие или меньшие напряжения. [c.312]
Нормальная сосредоточенная сила в бесконечной плоскости. [c.158]
Жидкости и газы всегда подвержены действию некоторых сил, которые являются в основном распределенными, т. е. приложенными во всех точках поверхности или объема. Однако в исключительных случаях в жидкостях могут действовать и сосредоточенные силы. Они возникают, например, как предельные значения распределенных сил, действующих на бесконечно малый жидкий объем, если его ускорение неограниченно возрастает. [c.56]
При подстановке нижнего предела правая часть в этом равенстве обращается в бесконечность при любом х, таким образом, сосредоточенная сила в плоской задаче вызывает бесконечные перемещения не только в точке ее приложения, что было бы естественно, но всюду. Эго обстоятельство представляется парадоксальным, по оно есть неизбежное следствие самой постановки плоской задачи. Как мы увидим далее ( 11.7), если сосредоточенная сила приложена к границе упругого полупространства, а не полуплоскости, парадокс исчезает, перемещения оказываются конечными всюду кроме точки приложения силы. [c.353]
Основное предположение линейной механики разрушения состоит в том, что трещина распространяется тогда, когда величина коэффициента интенсивности достигает критического значения, характерного для данного материала. Совершенно эквивалентная формулировка этого предположения состоит н том, что сила G, движущая трещину, превосходит критическое значение — сопротивление распространению трещины. Формула (19.4.4) утверждает эквивалентность двух этих формулировок. Что касается механического содержания принятой гипотезы и всей теории в целом, на этот вопрос можно ответить по-разному, а в рамках формальной теории вообще его можно не ставить. Тем не менее некоторые соображения могут быть высказаны. В оригинальной работе Гриффитса предполагалось, что освобождающаяся при росте трещины упругая энергия расходуется на увеличение поверхностной энергии если есть поверхностная энергия на единицу площади, то сила сопротивления движению трещины G = Анализ Гриффитса в течение долгих лет считался безупречным, хотя в нем содержится некоторый органический дефект. Энергия поверхностного натяжения вводится в уравнения теории как нечто данное и постороннее по отношению к упругому телу. На самом деле, поверхностная энергия есть энергия поверхностного слоя, свойства которого в той или иной мере отличаются от свойств остального материала и при решении задачи теории упругости этот поверхностный слой нужно как-то моделировать. Простейшая схема будет состоять в том, чтобы рассматривать поверхностный слой как бесконечно тонкую пленку с постоянным натяжением 7. Если контур свободного отверстия имеет кривизну, то поверхностное натяжение дает нормальную составляющую силы на контуре. При переходе к разрезу, в вершине которого кривизна становится бесконечно большой, поверхностное натяжение создаст сосредоточенные силы. В результате особенность у кончика трещины оказывается более высокого порядка, а именно, вида 1/г, а не 1/У г. На это обстоятельство было обращено внимание Гудьером, однако полное решение задачи было опубликовано много позже. В связи с этим можно выразить сомнение, связанное с тем, в какой мере пригодно представление о поверхностном натяжении в твердом теле как о натянутой бесконечно тонкой пленке, а особенно в какой мере эта идеализация сохраняет смысл при переходе к пределу, когда отверстие превращается в бесконечно топкий разрез. [c.664]
Из решения (76) для одной сосредоточенной силы, можно с помощью суперпозиции найти решения для других видов нагружения. Рассмотрим, например, случай (рис. 80), когда две равные но величине и противоположные ио знаку силы действуют на бесконечную пластинку в точках О и 0 , находящихся на очень малом расстоянии d друг от друга. Напряжения в любой точке М получаются с помощью суперпозиции напряжений, вызываемых силой в точке 0 и напряжения, вызываемых другой силой в точке О. Рассматривая, наиример, элемент в точке М, перпендикулярный оси х, и обозначая через [c.142]
Если требуется исследовать нагружение на границе отверстия, которое имеет ненулевые результирующие усилие и момент, можно исходить из решения для сосредоточенной силы, представленного в части (ж) задачи 2 на стр. 197, придавая силе требуемое результирующее значение. Сюда можно добавить решение для момента, представленное в части (а) той же задачи, считая Ь равным бесконечности и а — очень малым. Эти решения отвечают нагрузке, действующей на границе отверстия, которая обладает заданными результирующей силой и результирующим моментом, но распределена иначе, чем требуется. Заданное распределение нагрузки достигается введением некоторого доступного определению нагружения на границе отверстия, причем задача о таком нагружении отвечает требованиям, вытекающим из свойств аналитических потенциалов. [c.219]
Эпюры, построенные по этим формулам, представлены на рис. 10.25. Как видим, в центре изгибающие моменты обращаются в бесконечность, что является следствием того, что здесь обращается в бесконечность поперечная сила Q. В центре, таким образом, имеет место, как говорят, неустранимая особенность. В реальных условиях сосредоточенных в точ- [c.418]
Любая конструкция является системой с бесконечно большим числом степеней свободы, так как силы ее веса распределены по ее объему. Однако приближенный расчет конструкции даже в том случае, когда нельзя пренебречь ее весом, можно выполнить как расчет системы с одной степенью свободы. Для этого вес Q конструкции заменяют весом Q, сосредоточенным в некоторой точке. При вынужденных колебаниях эта точка принимается совпадающей с местом приложения возмущающей нагрузки. [c.534]
Плоская задача. Пусть к противоположным берегам прямолинейной сквозной трещины длиной 21, находящейся в бесконечной пластине, приложены равные и противоположно направленные сосредоточенные силы Р сила Р действует в середине трещины перпендикулярно к ее поверхности. На бесконечности напряжение отсутствует. При помощи (338) находим главный вектор нагрузок, приложенных к дуге AB со стороны нагретой области S (см. рис. 26) [c.111]
Пусть к противоположным поверхностям круговой дискообразной трещины радиуса R, находящейся в бесконечном теле, приложены равные и противоположно направленные сосредоточенные силы Р сила Р действует по оси круглой дискообразной трещины. В этом случае [c.112]
Здесь t x,y) — точка области Q С( ,л) — точка контура Г с(лС)=/- / /-/(8лЛ)- фундаментальное решение для задачи изгиба бесконечной пластины г = — х + у — т)) р(С) — интенсивность распределенной нормальной нагрузки />, — модуль сосредоточенной силы, приложенной в точке = 1,2,., и). [c.11]
Перемещения и деформации точки t(x.y) бесконечной пластины от действия сосредоточенной силы приложенной в точке С( ,п), определяются по формулам [6] [c.29]
Тангенциальные усилия Г,, Т , в бесконечной пластине от действия сосредоточенной силы р[р ,р определяются по формулам (1.6.7), которые с учетом (1.10.21) записываются в виде [c.40]
Подставляя (4.2 2) е уравнения (4.1.9), получаем формулы для определения тангенциальных усилий в бесконечной пластине при действии единичной сосредоточенной силы в направлении оси (Л = 1,2) [c.112]
Усилия на контуре Г, выделенном в бесконечной пластине, от действия единичной сосредоточенной силы определяются по формулам (4.1.10), которые с учетом (4.2.3) принимают вид [c.112]
Подставляя (4.2.12) в уравнения (4,1.9), (4.1.10), получаем формулы для определения усилий и поворотов в бесконечной пластине при действии единичной сосредоточенной силы, перпендикулярной пластине [c.114]
Замечание. Представляется естественным интерпретировать решение задачи 3 как расчет оболочки, дополнительно закрепленной в точке = О (вследствие чего там и возникает реакция). Однако такое представление весьма условно, так как по безмоментной теории под сосредоточенными силами перемещения обращаются в бесконечность ( 16.28). [c.249]
Вычисление средней мощности произведено в соответствии с формулой (5.8). Поскольку эта мощность определяется только мнимой частью в выражении нормального смещения (совпадающая по фазе с нагрузкой часть скоростей точек ее приложения), то бесконечный интеграл в (3.7) не вносит никакого вклада в эти величины. В случае сосредоточенной силы именно данный интеграл обеспечивает обращение в бесконечность смещения (скорости) в точке приложения силы. Это обусловливает обращение в бесконечность мгновенной мощности, развиваемой сосредоточенной силой при возбуждении полупространства, в то время как средняя за период мощность остается ограниченной. [c.104]
Используя фундаментальные результаты решения пространственной задачи [74, 104], находим, что средняя за период мощность Wo, излучаемая сосредоточенной силой Q ехр (—iwt) в бесконечную упругую среду, определяется по формуле [c.107]
В материале с величиной v = 0,25 при генерации колебаний сосредоточенной силой основная часть энергии (91%) уносится в бесконечность сферической волной сдвига. В двумерном случае (цилиндрические волны) возрастает интенсивность продольной волны, она уносит уже 25% общей энергии, подводимой от источника. [c.107]
В работе [1.13] исследованы закономерности усиления шума, создаваемого винтом на режиме висения при больших концевых числах Маха. Отдельно исследовались составляющие шума от толщины, подъемной силы и скачков уплотнения. Установлено, что концевая часть каждой из лопастей производит в неподвижной точке наблюдения импульсный шум, сосредоточенный в узкой зоне и повторяющийся с частотой прохождения лопастей. Исследовались изменения звукового давления по» мере уменьшения относительной толщины лопасти т до нуля. Одновременно неограниченно увеличивалось удлинение лопасти А, с тем, чтобы произведение гХ оставалось порядка 1 (в противном случае при возрастании X до бесконечности и фиксированном т импульсные составляющие от отдельных лопастей в составе шума не выделяются), а при М1 параметр околозвукового подобия (1—М)1х 1 оставался порядка 1. Уровень звукового давления внутри и вне указанной выше узкой зоны изменялся при изменении т или (1 — пропорционально различ- [c.867]
В кинематике сплошных сред, наряду с принятыми в кинематике дискретной системы точек понятиями перемещений, скоростей и ускорений, появляется характерное для сплошной среды представление о бесконечно малой деформации среды, определяемой тензором деформаций. Если рассматривается непрерывное движение текучей среды, то основное значение приобретает тензор скоростей деформаций, равный отношению тензора бесконечно малых деформаций к бесконечно малому промежутку времени, в течение которого деформация осуществилась. Как с динамической, так и с термодинамической стороны модель сплошной среды отличается от дискретной системы материальных точек тем, что вместо физических величин, сосредоточенных в отдельных ее точках, приходится иметь-дело с непрерывными распределениями этих величин в пространстве — скалярными, векторными и тензорными полями. Так, распределение массы в сплошной среде определяется заданием в каждой ее точке плотности среды, объемное силовое действие — плотностью распределения объемных сил, а действие поверхностных сил — напряжениями, определяемыми отношением главного вектора поверхностных сил, приложенных к ориентированной в пространстве бесконечно малой площадке, к величине этой площадки. Характеристикой внутреннего напряженного состояния среды в данной точке служит тензор напряжений, знание которого позволяет определять напряжения, приложенные к любой произвольно ориентированной площадке. Перенос тепла или вещества задается соответствующими им векторами потоков. [c.9]
Рассмотрим теперь бесконечную изотропную тонкую пластину, изготовленную из идеального упругопластического материала с одной прямолинейной трещиной длиной 21 [57]. Берега трещины свободны от внешних усилий. К пластине приклепаны поперечные ребра жесткости в точках Z = L i o- Выбор системы координат и обозначения поясняются на рис. 2.7. На бесконечности действует однородное растягивающее напряжение Оу = оо. Действие приклепанных подкрепляющих ребер на схеме заменено четырьмя сосредоточенными силами, приложенными в местах расположения заклепок (рис. 2.7). Материал пластины будем считать удовлетворяющим условию пластичности Треска—Сен-Венана, согласно которому [c.98]
Контур 2 составлен окружностью большого радиуса с центром в начале координат, берегами разрезов и двумя малыми окружностями с центром в вершинах трещин. Г-интеграл по большой окружности равен нулю, так как напряжения на ней убывают, как 1/г (сосредоточенная сила в бесконечной плоскости). Считаем, что материалы 1 и 2 находятся в упругом состоянии. На основании (3.17) находим [c.49]
Пластина растягивается на бесконечности напряжениями o i и 0Г2, в результате этого в заклепках появляются сосредоточенные силы Р, растягивающие подкрепляющий стержень постоянного поперечного сечения с площадью Sp (рис. 70, б). При Xi / стержень в теории будем считать бесконечным, однако это предположение не играет существенной роли, так как при удалении от места приложения силы напряжения в этой части стержня убывают очень быстро, так что уже на расстояниях порядка одного-двух диаметров поперечного сечения стержня ими можно пренебречь (т.е. можно считать стержень коротко обрубленным с обоих концов). Материал стержня и пластины, вообще говоря, разный. [c.159]
Если же составить ряд для изгибающих моментов (6.51), то он будет сходиться значительно медленнее, чем для прогибов, в особенности вблизи приложения силы Р, а непосредственно под силой он вообш е расходится — здесь моменты стремятся к бесконечности. Дело здесь не только и не столько в недостатках данного метода решения. Причина данной особенности состоит в самой модели силы, сосредоточенной в точке (рис. 6.29). Если из пластины вырезать вокруг точки приложения силы элемент х х Ai/ и устремить Аа О и Ау то для уравновешивания конечной силы Р интенсивность поперечных сил и моментов Qy, М , Му на гранях этого элемента должна будет возрастать до бесконечности. Действительно, пусть, например, из [c.173]
Сосредоточенные нагрузки. Как легко проверить из выражений (3.9ж) и (3.9з), сосредоточенная сила (сосредоточенная в плог скости пластины, но равномерно распределенная по ее толщине), приложенная в вершине клинообразной бесконечной пластины (рис. 3.12, а) или к краю полубесконечной пластин>1 (которую [c.173]
Движение под действием сосредоточенной силы. —Другой существенный пункт различия между струной и мембраной заключается в реакции на приложенную силу. Струна длиной I, рттянутая в сторону с помощью силы, сосредоточенной в точке х, вмеет форму, которая выражается двумя отрезками прямой, ак это изображено на фиг. 35. Форма эта такова, что сумма двух вертикальных компонент натяжения в точке приложения Thjx и Тк1 1 — х)] даёт силу Р. Смещение к = Ех 1 — х)1Т1 в точке приложения силы равно конечной величине, пропорциональной силе Р. В противоположность этому мембрана не может противостоять силе, сосредоточенной в точке смещение в точке приложения силы оказывается бесконечным, как бы мала ни была эта сила. Например, если бы сила была сосредоточена в центре круглой мембраны радиуса а, то смещение т) точки, лежащей на расстоянии г о г хдентра, было бы равно = (2 /7 ) 1п ( // ) (где 1п означает натуральный логарифм ). Эго выражение является решением уравнения (17.2) для случая равновесия (т. е. когда правая часть уравнения (17.2 равна нулю). Оно становится равным нулю при г = а и равным бесконечности при г = 0. [c.199]
Как ВИДИЛ1, в точке приложения силы имеется особенность в перемещениях они, как и напряжения, стремятся к бесконечности. Это, как уже указывалось, является следствием схематизации сосредоточенной силы, приложенной в точке. Если воспользоваться выражениями (4.112) или (4.110), (4.111) как функциями влияния, то по выражению типа (4.108) от распределенной нагрузки, приложенной к краю, получим конечные перемещения. [c.120]
Задачу о действии сосредоточенно силы на границе полуплоскости можно рассматривать как распространение случая нагружения бесконечного клина в вершине силой Р в предполон ении, что угол раствора клина равен л, т. е. а = л/2. [c.108]
Если, кроме сосредоточенных расклинивающих сил, приложенных в серединах сторон щели, упругая плоскость находится под действием всестороннего сжатия с напряжением р = onst в бесконечности. [c.523]
Здесь 6 у) Н у)—дельта-функция Дирака. (Относительно обобщенных функций см. работу Лайтхилла [21] ).) Таким образом, растягивающее усилие Т равно нулю всюду, за исключением двух граничных волокон (т. е. поверхностей), где оно обращается в бесконечность, что соответствует сосредоточенным силам, приложенным к этим волокнам. На верхнее во- локно действует сосредоточенное растягивающее усилие, равное (F/D) (L — х), на нижнее — сжимающее усилие той же величины. Поскольку нижняя поверхность не опирается на основание, препятствующее выпучиванию волокна из материала, мы [c.295]
| Рис. 12.90. Бесконечная балка на сплошном.упругом основании а) балка, загруженная сосредоточенной силой б) основная система в виде двух полубесконечных балок в) использование результата, относя1дегося к бесконечной балке, загруженной сосредоточенной силой для отыскания эффекта действия произвольной нагрузки г) эпюра V в роли линии влияния прогиба в сечении под сосредоточенной силой / — линия прогиба бесконечной балки на упругом основании при действии силы, равной единице, в точке А 2 — то же при действии силы, равной единице, в точке В кривая 1 полностью совмещается с крн вой 2 при смещении вправо на расстояние а. Поскольку = В А) (первый индекс — |  |
Сосредоточенная сила в вершине клина. Рассматриваемая клинообразная бесконечная область ограничена двумя полупрямыми у = rtxtga под углом 2а ось Ох направлена внутрь этой области, а начало координат (вершина клина) принято за начало полярной системы координат (г, 9), так что —аПроекции силы, приложенной в вершине клина, на оси Ох, Оу обозначаются X, У грани клина предполагаются ненагружен-ными [c.531]
Тангенциальные усилия в бесконечной пластине от действия сосредоточенной силы Л) определяются в лока 1ьной системе координат /). т по формулам [c.29]
Здесь поперечная сила имеет в граничной точке х = / особенность, связанную со спецификой метода. Она возникает из-за того, что в этой точке прикладывается сосредоточенный момент. Для того чтобы придать конечное значение поперечной силе, надо ограничиться предельным значением х->/-0, в котором точка х стремится бесконечно близко к точке /, не достигая ее. В этом случае значение 3(-0) = 0. Аналогичная ситуация возникает при применении метода граничных элементов в задаче изгиба пластин. Там поперечная сила выражается через суперсингулярный интеграл, которому придается конечное значение в смысле Адамара. [c.186]
Остановимся кратко на задачах включения для цилиндрической оболочки. Для пластин эти задачи детально обсуждены в первых трех главах книги. Что 1 касается круговых цилиндрических оболочек, то работ в этой области немного. Можно сослаться на статью Ф. Фишера [75], в которой исследован случай бес- конечно длинной круговой цилиндрической оболочки с бесконечно длинным реб-ром, нагруженным в начале координат продольной сосредоточенной силой (ана- лог задачи Е. Мелана для пластины). Решение задачи стронтси путем разреза-ния оболочки по линии присоединения ребра. Получается незамкнутая панель,, к уравнениям которой сначала применяется преобразование Фурье по продоль- Ной координате. После этого интегрируются обыкновенные дифференциальные уравнения. Константы определяются в явном виде из условий стыковки с реб- > ром для изображения. Трудность, как обычно, состоит в вычислении интегралов. обратного преобразования. Это делается комбинированием квадратурных формул. и асимптотических разложений. Показано, что решеняе по теории пологих оболочек и теории И. Снмондса [82] практически совпадает. Эта задача с учетом изгиба ребер в цитированной статье Ф. Фишера решена впервые. Характер особенностей решения в окрестности приложенной силы, однако, в работе не выведен. Но можно отметить, что как и в задаче Мелана, касательные усилия взаимодействия между ребром и оболочкой будут иметь логарифмическую особен- ность в точке приложения силы. К задаче включения можно приписать и задачу [c.322]
Сосредоточенная нагрузка, приложенная к углу. Рассмотрим в качестве примера случай вертикальней реакции Р (силы, отнесенной к толацине пластины), которая приложена к нижнему углу балки, которую будем считать бесконечно высокой и длинной, как показано йа рис. 3.12,6. Постоянные А п В можно определить из условия равновесия свободного тела, на которое дейстаует сила Р, например на часть тела, которая на рисунке заштрихована и расположена слева от линии х = а. Расстояние а должное быть конечным, так как напряжения обращаются в бесконечность в начале координат, поэтому при бесконечном а приходится ньГеть дело с неопределенными величинами. . [c.174]
Влияние свободных поверхностей учитывают с помощью функций в виде полиномов в сочетании с техникой конформных отображений. При этом комплексная переменная г, соответствующая геометрии трещины, выражается как функция другой комплексной переменной g, соответствующей геометрии единичного круга или полуплоскости в бесконечном теле. Иллюстрация этого метода дана Парисом и Си [7], рассмотревшими действие единственной сосредоточенной силы F, направленной под произвольным углом к поверхности трещины. Для представления полей растягивающих и сдвиговых напряжений у вершины трещины, возникающих благодаря этой силе, ими был использован комплексный коэффициент интенсивности напряжений К = К — iK , и после формального вывода Стц и сГзг из полной комплексной функции напряжений Вестергаарда с использованием переменной т] = (z—вместо действительного расстояния г = (Xi — а) [как в выводе уравнения (115) из (ПО)] они смогли записать [c.75]
Сосредоточенные нагрузки (силы и моменты сил)
Выделим на участке, где нет сосредоточенных сил и моментов, малый элемент балки О О — Он находится в равновесии под действием внешней нагрузки, поперечных сил и изгибающих моментов в сечениях Oi и О2 (рис. 64, б). Поскольку в общем случае Q и УИ меняются вдоль оси балки, то в сечении Oi имеем Q (х) и М (х), а в сечении О2 имеем Q (х) + dQ и М (х) + dM. Для вывода, как всегда, изображаем их положительно направленными. Из условия равновесия выделенного элемента получим [c.54]Найти характерные сечения балки. Характерными сечениями считаются те, в которых приложены сосредоточенные силы и моменты, начинается или заканчивается распределенная нагрузка, а также те, в которых Q обращается в нуль. [c.60]
На балку АВ действуют три нагрузки в точке А — сосредоточенная сила /»и момент Т, а на участке СВ=6 м — равномерно распределенная нагрузка интенсивностью д, которую заменим равнодействующей приложенной в точке О — посередине участка СВ. Следовательно (рис. 116, б), [c.116]
Для решения нелинейных задач статики гибких стержней необходимо знать поведение внешних нагрузок в процессе деформации стержня, а также необходимо учитывать изменение краевых условий, например перемещение шарнира (рис. 1.2). Конечное состояние гибкого стержня будет различным, если, например, нагружать стержень в одном случае мертвой- силой ( мертвой называется нагрузка, сохраняющая при деформации системы свое направление), а в другом — следящей, т. е. силой, которая в процессе деформации стержня сохраняет свое направление по отношению к стержню, например образует неизменные углы с подвижными осями. В более общем случае нагружения на стержень кроме сосредоточенных сил и моментов могут действовать и распределенные силы и моменты. [c.15]
Рассмотрим более подробно возможные случаи поведения внешней нагрузки (распределенных и сосредоточенных сил и моментов), входящих в векторные уравнения (1.31), (1.32). Уравнения (1.31) — (1.35) справедливы для больших перемещений [c.23]
Уравнения равновесия (6.91) —(6.102) получены в осях, связанных с линией центров жесткости. В предыдущих задачах считалось, что центр жесткости и центр тяжести сечения совпадают, или считалось, что линии действия распределенных сил и моментов q и р, сосредоточенных сил Рлинию центров жесткости. Аэродинамическая нагрузка приводится к центру тяжести сечения, поэтому при приведении ее к центру жесткости сечения появляется дополнительный распределенный момент n q Xa (а = —аез), поэтому полный распределенный момент, входящий в уравнение (6.94), [c.257]
Вывод уравнений. Рассмотрим стержень (рис. 6.6), нагруженный сосредоточенной силой и моментом, с учетом случайных составляющих АР и АТ. Действующая на упругие элементы, например, распределенная случайная нагрузка Ад (зависящая от Аа) вызовет появление случайных составляющих векторов, характеризующих напряженно-деформированное состояние стержня [c.142]
Помимо распределенной нагрузки к балке приложены сосредоточенные силы в тех сечениях, где на эпюре Q имеются скачки, и сосредоточенные моменты в местах скачков на эпюре М. Значения и направления сосредоточенных сил и моментов можно определять по следующим формулам, которые получены из рассмотрения равновесия элемента балки длиной dz, выделенного двумя сечениями слева и справа от скачков на эпюрах Q и М [c.105]
Результаты многочисленных точных и приближенных решений убеждают в том, что фактический способ приложения силы и момента к концу стержня сказывается лишь в непосредственной близости к этому концу. В данном случае это означает, что если нас интересуют прогибы и удлинение балки в целом, нам нет необходимости детально анализировать реальную ситуацию, изображенную на рис. 1.5.3, а, при расчетах достаточно исходить из упрощенной схемы, представленной на рис. 1.5.3, б, которая носит совершенно условный характер, поскольку ни сосредоточенных сил, ни сосредоточенных моментов не существует. Область, в которой сказывается фактический способ приложения нагрузки, заштрихована на рисунке, границы этой области тоже условны вне ее состояния, соответствующие статически эквивалентным нагрузкам, отличаются достаточно мало. Что значат слова достаточно мало , мы пока не уточняем. Высказанное правило носит название принципа Сен-Венана, довольно расплывчатая формулировка связана с тем, что этот принцип не доказывается для общего случая, а иллюстрируется многочисленными примерами. [c.27]
Заметим, что при применении метода Рэлея требование удовлетворения функцией v z) всех граничных условий является излишним. Разрывы вторых производных функций и (г) соответствуют приложенным сосредоточенным моментам, разрывы третьих производных — сосредоточенным силам. Следовательно, если функция v z) непрерывна вместе с первой производной и удовлетворяет граничным условиям, наложенным на прогиб и угол поворота, она всегда может быть представлена как функция прогиба некоторой балки под действием распределенной нагрузки, сосредоточенных сил и моментов и доказательство теоремы Рэлея сохраняет силу. Будем называть граничные условия, налагаемые на v z) и v z) кинематическими условиями, а на момент и перерезывающую силу, т. е. на и» (z) и и » (z) — динамическими условиями. [c.203]
Рассмотрим один из методов численного решения линейных дифференциальных уравнений — метод начальных параметров. Изложенный ниже метод справедлив не только для стержня, нагруженного по всей длине распределенной нагрузкой, но и для общего случая нагружения, когда распределенная нагрузка приложена к части стержня и, кроме того, действуют сосредоточенные силы и моменты (см. рис. В.11) [c.196]
Указание. Каждая из задач может быть решена по методу сил с применением- способа группировки нагрузок на симметричные и антисимметричные составляющие или с применением способа аналогий. Кроме того, при произвольном числе сосредоточенных нагрузок—сил и моментов — можно каждую задачу решить, комбинируя решения задач а), б), в) для отдельных нагрузок. Этот способ применим и тогда, когда нагрузки образуют систему уравновешенных сил при суммировании действий отдельных нагрузок влияние распределенных реакций д (р) автоматически исключаете . [c.383]
Перемещения (прогибы и углы поворота) системы в результате ее деформации условимся обозначать А , где индекс т указывает направление перемещения, а п — причину, вызвавшую его. Таким образом, А , — перемещение по направлению силы т, вызванное силой п. Перемещение А , может представлять собой либо линейное смещение, либо угол поворота (в радианах) в зависимости от того, является сила т сосредоточенной силой или сосредоточенным моментом. Под силой п понимается любая нагрузка, действующая на сооружение, например нагрузка, состоящая из нескольких сосредоточенных сил и моментов и какой угодно распределенной нагрузки. [c.429]
Если внешняя распределенная нагрузка q отсутствует, правая часть уравнения обращается в нуль, а сосредоточенные силы и момент учитываются путем наложения соответствующих граничных условий при определении постоянных интегрирования. [c.170]
Обозначают характерные сечения балки. Ими являются концевые сечения балки, опоры, точки приложения сосредоточенных сил и моментов, начало и конец распределенной нагрузки. [c.33]
Выводы о взаимосвязи эпюр М и Q между собой и с внешней нагрузкой позволяют обходиться без составления уравнений изгибающих моментов и поперечных сил для каждого участка балки. Достаточно вычислить ординаты эпюр для характерных сечений И соединить их линиями в соответствии с изложенными вьпие правилами. Характерными являются сечения балки, где приложены сосредоточенные силы и моменты (включая опорные сечения), а также сечения начала и конца участков с равномерно распределенной нагрузкой. Для определения максимальных значений изгибающих моментов дополнительно вычисляют моменты в сечениях, где поперечные силы равны нулю. Вычисления при этом менее трудоемки, чем при построении эпюр по уравнениям. [c.106]
Итак, внешняя нагрузка, действующая на стержень и вызывающая его поперечный изгиб в плоскости Oyz складывается из распределенных силовой и моментной нагрузок ду и и сосредоточенных сил и моментов Ру, Ш . При этом указываются участки, на которых имеет место та или иная распределенная силовая или моментная нагрузка и координата сечения приложения сосредоточенной силы или сосредоточенного момента. [c.202]
Разумеется, что точки, в которых у рассчитываемого стержня имеется излом оси и (или) ступенька в поперечных сечениях (в форме и (или) размерах), принимаются в качестве узлов обязательно. Если на рассчитываемый объект действуют внешние сосредоточенные силы и моменты, то и точки их приложения также принимаются в качестве узлов. Распределенные же силовая и моментная нагрузки приводятся к узлам, принятым на основе вышеизложенных соображений, или, если они оказываются слишком редкими, то —и к специально для этой цели введенным узлам. Таким образом, распределенные нагрузки сводятся также к сосредоточенным силам и моментам. [c.355]
| Рис. 2.56. Нормальные силы и моменты в ребрах и в верхних поясах диафрагм модели при сосредоточенных нагрузках Р=1600 Н а — места приложения нагрузок б — силы и моменты в ребрах и в диафрагме при нагрузке в точке 3 в — силы и моменты в ребрах и в диафрагме при нагрузке в точке 4 |  |
Показано, что при введении условной упруго вязкой схемы для учета малого внутреннего трения пригодна известная методика с использованием функций и интегралов А. Н. Крылова. Приведешь соответствующие решения для случаев нагрузки балки сосредоточенными силами и моментами. Дана числовая оценка. Библ. 6. [c.222]
Комбинируя случай нагружения части балки равномерно распределенной нагрузкой со случаями нагружения сосредоточенной силой и моментом на концах участка, можно получить расчетные величины для балки ограниченной длины. [c.68]
Для определения кривых прогибов трубопровода выбираем точку приведения, нагружаем систему в этой точке сосредоточенной силой, освобождаем один из концов трубопровода и с помощью способа переноса сил и моментов определяем нагрузку на каждый из участков трубопровода. Интегрированием уравнения кривой статического прогиба (в которой должны быть учтены перемещения всех участков трубопровода по трем осям координат) находим. приведенную массу трубопровода. Приведенный коэффициент [c.193]
Для стержней сосредоточенными нагрузками являются силы и пары сил (моменты), что показано на рис. 1.22, а, б. Сосредоточенная сила имеет размерность Н, кН, а сосредоточенный момент — соответственно Нм, кНм. По отношению к оси стержня все нагрузки можно привести к осевым (рис. 1.23, а), поперечным (рис. 1.23,6) и скручивающим (рис. 1.23, в) составляющим. [c.16]
Формула (16.27.2) составлена в предположении, что в верхнем полюсе географической системы координат, т. е. в точке S = О, оболочка, вообще говоря, будет испытывать действие силы и момента. Однако (16.27.2) остается в силе и в случае, когда точка S = О не загружена. Для этого надо только выбирать силы и моменты, приложенные в точках = р, так, чтобы они были в совокупности уравновешены. При этом в точке S = О сосредоточенные силы и моменты будут отсутствовать. Более существенно принятое выше предположение, что ни одна из точек приложения сосредоточенных сил и моментов не совпадает с нижним полюсом географической системы координат ( р = оо). Поэтому задачу о построении комплексной функции напряжения для случая, когда сосредоточенная нагрузка действует в точке = оо, надо рассмотреть отдельно. [c.237]
Поправки, которые вносит локальный краевой эффект в окрестности точки приложения нагрузки, имеют не только количественный, но и качественный характер. Он меняет порядок особенностей функций, определяющих перемещения, усилия и моменты оболочки. А именно, за счет локального краевого эффекта происходит снижение порядка особенностей. Для общего случая порядок особенностей в перемещениях, усилиях и моментах оболочки под сосредоточенными воздействиями разобран в работе [132]. Для сферической оболочки этот вопрос обсуждался в статье [40]. Там же задача действия на сферическую оболочку произвольной системы сосредоточенных сил и моментов решена по моментной теории точно (в замкнутой форме). [c.244]
Это значит, что предложенным способом поставленная задача не всегда может быть решена. Надо требовать, чтобы действующая на оболочку сосредоточенная нагрузка удовлетворяла условиям, вытекающим из (17.30.9) и из формул (16.26.14), связывающих константы Oj, Оо, a i с компонентами сосредоточенной силы и момента. Эти условия записываются так [c.247]
Схема нагрузки вала сосредоточенными силами и моментами (рис. 5.19, б) показывает, что вал работает на изгиб в вертикальной плоскости, изгиб в горизонтальной плоскости и кручение. Рассмотрим каждую деформацию отдельно, пользуясь при-нцшюм независимости действия сил. [c.172]
Подставляя в уравнение для функции напряжений (10.6.8), мы получим дифференциальное уравнение четвертого порядка для функций / , одинаковое как для решения Рибьера, так и для решения Файлона. Каждая из функций / будет зависеть от четырех констант. Представляя заданные при Х2 = 6 нагрузки или перемещения формально рядами по косинусам или синусам аргумента, кратного nxjl, мы находим эти константы таким образом, граничные условия на длинных сторонах оказываются удовлетворенными. Подчеркнем еще то, как это уже делалось неоднократно, что ряды Фурье для заданных величин нагрузок вовсе не обязательно должны быть сходящимися, нагрузки могут быть разрывными и даже содержать дельта-функции и.чи производные от них (сосредоточенные силы и моменты). [c.355]
Ось балки направляется по оси х оси совмещаются с главными осями сечения у (вертикальная) и z (горизонтальная). Обозначения внешних нагрузок сосредоточенные силы Р в кГ или т сосредоточенные моменты L в кГсм или тм , интенсивность сплошной нагрузки р х) в кГ1м, где X — координата сечения балки. Проекции сил и нагрузок, направленных вниз, считаются положительными, и наоборот. Опорные реакции (силы и моменты) после их определения рассматриваются как в(1ешняя нагрузка. [c.50]Обозначения и правило знаков для р, Q и М—см. фиг. 13, а. Уравнения для Q(x) и М(х) составляются отдельно для каждого участка балки последовательным интегрированием эпюр р (х) и Q (х) по формулам (54). За участок балки принимается каждая ее часть между соседними сосредоточенными силами и моментами, имеющая один закон сплошной нагрузки р (х). Начальные па раметры Q (0) и М (0) — значения Q и М в сечении л = О (или на границау у част ков) опорные реакции определяются с помощью уравнений статики (см. т. I, гл. XVI11, стр. 352). [c.51]
В истеме уравнений (3.3)—(3.4) неизвестными являются векторы Q и ЛТ, известными — действующие распределенные нагрузки, а также сосредоточенные силы и моменты, приложенные к стержню (см. рис. 3.1), и условия закрепления стержн . Система уравнений (3.3)—(3.4) не является полной, так как определить Q и Л1 из этой системы в общем случае нельзя. Дело в том, что в уравнение (3.4) входит единичный вектор натурального триедра, положение которого [c.68]
Рассмотрим содержание ее правой части. Первый столбец формул показывает, что потенциальная энергия деформации равна половине произведения силы или момента пары сил на перемеитенпе того сечения, где эта сила или соответственно пара сил приложены. Условимся называть термином обобщенная сила любую нагрузку, вызывающую деформацию, т. е. и сосредоточенную силу, и момент пары сил. Перемещение же, соответствующее этой обобщенной силе, будем называть обоби снным перемещением. Соответствие заключается в том, что речь идет о перемещении сечения, где приложена сила, причем о таком перемещении, произведение которого на эту силу дает величину работы. Для сосредоточенной силы это будет линейное перемещение по направлению действия силы удлинение, прогиб для пары сил угол поворота по направлению действия момента пары. Формулы первого столбца можно обобщить так потенциальная энергия деформации численно равна половине произведения обобщенной силы на обоби енное перемеш ение. [c.313]
К балке приложены активные силы и моменты. Это — сила тяжести балки Р, которая приложена посредине балки, заданная сила F, пара сил с моментом М и равномерно распределенная по участку КВ нагрузка q. Вместо равномерно распределенной нагрузки удобнее рассмотреть сосредоточенную силу Q, равную по мо/дулю Q = q КВ = 0,5 Н/м 3 м = 1,5 PI и приложенную посредине участка ATjB. На расчетной схеме мы не будем изображать равномерно распределенную нагрузку, а заменим ее силой Q. (В сущности, мы уже не раз пользовались в задачах подобной заменой, когда изображали вес балки посредине балки — ведь силы тяжестрг тоже равномерно распределены по длине балки.) [c.59]
Набор концентрированной силы
| Elder Scrolls Online Wiki
- Вики Главная
- Вики-дом
- Сообщество и социальные сети
- Медиа и искусство
- Галерея
- Фан-арт
- Индекс потоков
- Чат
- Форум
- Гильдии
- ID игроков
- Пар
- PlayStation
- Xbox
- ESO Reddit
- Медиа и искусство
- Вики-форумы
- Wiki To-Do
- Wiki Shop
- Блог Fextralife
- Fextralife Wiki Hub
- Общая информация
- Общая информация
- О The Elder Scrolls Online
- Tamriel Unlimited (модель B2P)
- Учебники
Описание обновления - DLC
- Органы управления
- Эмоции и жесты
- Combat
- Гильдии
- Кронный магазин
- Крепления
- Отличия консоли и ПК
- Часто задаваемые вопросы
- Информация о персонаже
- Информация о персонаже
- Гонки
- Классы
- Некромант
- Рыцарь Дракона
- Ночной клинок
- Колдун
- Тамплиер
- Надзиратель
- Статистика
- Скорби
- Камни Мундуса
- Система чемпионов
- Фракции
- Ковенант Даггерфолла
- Эбонхартский пакт
- Альдмерский Доминион
- Строит
- PvE Строит
- PvP Строит
- Навыков
- Навыки
- Навыки чемпиона
- Навыки класса
- Навыки оружия
- Навыки брони
- Навыки гильдии
- Мировые навыки
- Навыки войны союзов
- Расовые навыки
- Навыки ремесла
- Оборудование
- Оборудование
- Наборы
- Броня
- Легкая броня
- Средняя броня
- Тяжелая броня
- Щиты
- Оружие
- Символы
- Красители
- Ремесло
- Создание
- Мотивы и стили
- Черты
- Алхимия
- Кузнечное дело
- Ткань
- Наложение чар
- Подготовка
- Изготовление ювелирных изделий
сосредоточенная сила — сила, действующая вдоль одной линии в пространстве. Сосредоточенные силы — полезные математические идеализации, но их нельзя найти в реальном мире, где все силы являются либо объемными силами, действующими в объеме, либо поверхностными силами, действующими в пределах…… Глоссарий по механике
сила — направленное взаимодействие между двумя объектами, которое имеет тенденцию изменять импульс обоих.Поскольку сила имеет направление и величину, ее можно выразить как вектор приложенной силы осевая сила сила тела тормозная сила сила развала центральная сила…… Глоссарий механики
сосредоточенная нагрузка — внешняя сила, которая является сосредоточенной силой… Словарь механики
Концентрация сил — это практика сосредоточения вооруженных сил, чтобы задействовать такую подавляющую силу против части вражеских сил, что несоответствие между двумя силами только действует как множитель силы в пользу сосредоточенные силы … Википедия
Force 136 — это общее прикрытие подразделения британской организации времен Второй мировой войны, Special Operations Executive (SOE).Отряд 136 действовал в регионах театра военных действий в Юго-Восточной Азии, которые были оккупированы Японией с 1941 по…… Wikipedia
force — принудительно, прил. беспомощный, прил. форсер, n. принудительно, нареч. / fawrs, fohrs /, n., v., принуждение, принуждение. п. 1. физическая сила или сила, которыми обладает живое существо: он использовал всю свою силу, чтобы открыть окно. 2. сила или мощь, проявленная к…… Универсалию
Концентрированная солнечная энергия — Солнечная электростанция PS10 концентрирует солнечный свет от поля гелиостатов на центральной солнечной электростанции.Системы концентрированной солнечной энергии (CSP) используют зеркала или линзы для концентрации большой площади солнечного света или солнечной тепловой энергии на…… Wikipedia
Концентрат — Концентрат Концентрат (? Или?), V. T. [Имп. & п. п. {Концентрированный}; п. пара & vb. п. {Концентрация}.] [Прив. con + L. centrum center. Ср {Concenter}.] 1. Привести или направить к общему центру; сплотиться теснее; собрать в … … Международный словарь английского языка
Силовое поле — Для использования в других целях, см Силовое поле (значения).Силовое поле, иногда называемое энергетическим щитом, силовым щитом или дефлекторным щитом, представляет собой концепцию сильно ограниченного поля значительной величины, так что объекты, на которые воздействует…… Wikipedia
Speed Force — Speed Force — это вымышленная концепция, представленная в различных комиксах, опубликованных DC Comics. Источник всей скорости Speed Force — это нечетко определенная экстрамерная энергетическая сила, от которой большинство сверхскоростных героев приводили в действие героев, таких как множественные…… Википедия
База ВВС Карсвелл — Инфобокс Название аэропорта = База ВВС Карсвелл собственное имя = ширина изображения = 300 caption = 31 января 1995 г. image2 width = caption2 = IATA = FWH ICAO = KFWH FAA = FWH type = Военный владелец = United States Air Расположение силы = Форт-Уэрт, штат Техас, построенный… Wikipedia
сосредоточенная сила — сила, действующая вдоль одной линии в пространстве. Сосредоточенные силы — полезные математические идеализации, но их нельзя найти в реальном мире, где все силы являются либо объемными силами, действующими в объеме, либо поверхностными силами, действующими в пределах…… Глоссарий по механике
сила — направленное взаимодействие между двумя объектами, которое имеет тенденцию изменять импульс обоих.Поскольку сила имеет направление и величину, ее можно выразить как вектор приложенной силы осевая сила сила тела тормозная сила сила развала центральная сила…… Глоссарий механики
сосредоточенная нагрузка — внешняя сила, которая является сосредоточенной силой… Словарь механики
Концентрация сил — это практика сосредоточения вооруженных сил, чтобы задействовать такую подавляющую силу против части вражеских сил, что несоответствие между двумя силами только действует как множитель силы в пользу сосредоточенные силы … Википедия
Force 136 — это общее прикрытие подразделения британской организации времен Второй мировой войны, Special Operations Executive (SOE).Отряд 136 действовал в регионах театра военных действий в Юго-Восточной Азии, которые были оккупированы Японией с 1941 по…… Wikipedia
force — принудительно, прил. беспомощный, прил. форсер, n. принудительно, нареч. / fawrs, fohrs /, n., v., принуждение, принуждение. п. 1. физическая сила или сила, которыми обладает живое существо: он использовал всю свою силу, чтобы открыть окно. 2. сила или мощь, проявленная к…… Универсалию
Концентрированная солнечная энергия — Солнечная электростанция PS10 концентрирует солнечный свет от поля гелиостатов на центральной солнечной электростанции.Системы концентрированной солнечной энергии (CSP) используют зеркала или линзы для концентрации большой площади солнечного света или солнечной тепловой энергии на…… Wikipedia
Концентрат — Концентрат Концентрат (? Или?), V. T. [Имп. & п. п. {Концентрированный}; п. пара & vb. п. {Концентрация}.] [Прив. con + L. centrum center. Ср {Concenter}.] 1. Привести или направить к общему центру; сплотиться теснее; собрать в … … Международный словарь английского языка
Силовое поле — Для использования в других целях, см Силовое поле (значения).Силовое поле, иногда называемое энергетическим щитом, силовым щитом или дефлекторным щитом, представляет собой концепцию сильно ограниченного поля значительной величины, так что объекты, на которые воздействует…… Wikipedia
Speed Force — Speed Force — это вымышленная концепция, представленная в различных комиксах, опубликованных DC Comics. Источник всей скорости Speed Force — это нечетко определенная экстрамерная энергетическая сила, от которой большинство сверхскоростных героев приводили в действие героев, таких как множественные…… Википедия
База ВВС Карсвелл — Инфобокс Название аэропорта = База ВВС Карсвелл собственное имя = ширина изображения = 300 caption = 31 января 1995 г. image2 width = caption2 = IATA = FWH ICAO = KFWH FAA = FWH type = Военный владелец = United States Air Расположение силы = Форт-Уэрт, штат Техас, построенный… Wikipedia
сосредоточенная сила — сила, действующая вдоль одной линии в пространстве. Сосредоточенные силы — полезные математические идеализации, но их нельзя найти в реальном мире, где все силы являются либо объемными силами, действующими в объеме, либо поверхностными силами, действующими в пределах…… Глоссарий по механике
сила — направленное взаимодействие между двумя объектами, которое имеет тенденцию изменять импульс обоих.Поскольку сила имеет направление и величину, ее можно выразить как вектор приложенной силы осевая сила сила тела тормозная сила сила развала центральная сила…… Глоссарий механики
сосредоточенная нагрузка — внешняя сила, которая является сосредоточенной силой… Словарь механики
Концентрация сил — это практика сосредоточения вооруженных сил, чтобы задействовать такую подавляющую силу против части вражеских сил, что несоответствие между двумя силами только действует как множитель силы в пользу сосредоточенные силы … Википедия
Force 136 — это общее прикрытие подразделения британской организации времен Второй мировой войны, Special Operations Executive (SOE).Отряд 136 действовал в регионах театра военных действий в Юго-Восточной Азии, которые были оккупированы Японией с 1941 по…… Wikipedia
force — принудительно, прил. беспомощный, прил. форсер, n. принудительно, нареч. / fawrs, fohrs /, n., v., принуждение, принуждение. п. 1. физическая сила или сила, которыми обладает живое существо: он использовал всю свою силу, чтобы открыть окно. 2. сила или мощь, проявленная к…… Универсалию
Концентрированная солнечная энергия — Солнечная электростанция PS10 концентрирует солнечный свет от поля гелиостатов на центральной солнечной электростанции.Системы концентрированной солнечной энергии (CSP) используют зеркала или линзы для концентрации большой площади солнечного света или солнечной тепловой энергии на…… Wikipedia
Концентрат — Концентрат Концентрат (? Или?), V. T. [Имп. & п. п. {Концентрированный}; п. пара & vb. п. {Концентрация}.] [Прив. con + L. centrum center. Ср {Concenter}.] 1. Привести или направить к общему центру; сплотиться теснее; собрать в … … Международный словарь английского языка
Силовое поле — Для использования в других целях, см Силовое поле (значения).Силовое поле, иногда называемое энергетическим щитом, силовым щитом или дефлекторным щитом, представляет собой концепцию сильно ограниченного поля значительной величины, так что объекты, на которые воздействует…… Wikipedia
Speed Force — Speed Force — это вымышленная концепция, представленная в различных комиксах, опубликованных DC Comics. Источник всей скорости Speed Force — это нечетко определенная экстрамерная энергетическая сила, от которой большинство сверхскоростных героев приводили в действие героев, таких как множественные…… Википедия
База ВВС Карсвелл — Инфобокс Название аэропорта = База ВВС Карсвелл собственное имя = ширина изображения = 300 caption = 31 января 1995 г. image2 width = caption2 = IATA = FWH ICAO = KFWH FAA = FWH type = Военный владелец = United States Air Расположение силы = Форт-Уэрт, штат Техас, построенный… Wikipedia
